مسئله رنگ آمیزی گراف Graph coloring

مسئله رنگ آمیزی گراف که با نام Graph coloring شناخته میشود ، مسئله کلاسیک در بهینه سازی ، طراحی الگوریتم و هوش مصنوعی است که کاربردهای فراوانی در دنیای واقعی دارد.

آشنایی با مسئله رنگ آمیزی گراف :

در این مسئله فرض بر این است که یک گراف با N گره یا راس داریم ، و میخواهیم راس های گراف را با m رنگی که در دست داریم رنگ آمیزی کنیم به شکلی که هیچ دو راس مجاوری رنگ یکسان نداشته باشند.

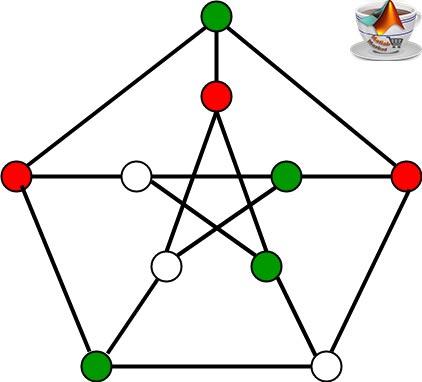
فرضیات مسئله به شرح زیر است :

• تعداد N گره یا راس داریم،
• تعداد M رنگ داریم ،
• تعداد رنگ ها کمتر از تعداد گره هاست
• هر گره باید با یک رنگ ، رنگ آمیزی شود،
• اگر دو گره به هم وصل شده باشند، نباید رنگ یکسانی داشته باشند.

برای آشنایی بیشتر با این مسئله به “بررسی جامع مسئله رنگ آمیزی گراف” مراجعه کنید.

در نظریه گراف، رنگ‌آمیزی گراف یکی از حالت‌های خاص مسئله‌های برچسب‌گذاری گراف است.

رویکرد کلی آن استفاده از نظیر کردن رنگهایی به یالها یا راس‌هاست که این رنگ‌آمیزی محدودیت خاصی را رعایت کند.

در ساده‌ترین حالت، رنگ‌آمیزی‌ای مورد نظر است که در آن هیچ دو راس مجاوری هم رنگ نباشند (رنگ‌آمیزی راسها).

علاوه بر آن رنگ‌آمیزی یالها به همین صورت تعریف می‌شود.

رنگ‌آمیزی گراف کاربردهای زیادی در زمینه‌های عملی و تئوری گوناگون دارد.

علاوه بر مسئله‌های کلاسیک تعریف شده در این زمینه، با در نظر گرفتن محدودیت‌های مختلفی روی نوع گرافها، روی روش رنگ‌آمیزی و حتی تعداد و رنگ عناصر گراف مسئله‌های متنوعی با کاربردهای وسیع در صنعت و علوم تعریف و حل می‌شود.

تعریف مسئله رنگ آمیزی گراف :

فرض کنید می‌خواهیم راس های گراف G را رنگ کنیم به صورتی که هیچ دو راس مجاوری یک رنگ نباشند ، کمترین تعداد رنگ مورد نیاز برای این کار را χ(G) می‌نامیم .

می ‌خواهیم الگوریتمی ارائه‌دهیم که χ(G) را بیابد و در حالت کلی تر گراف را آن را با این تعداد رنگ ، رنگ‌آمیزی کند.

تاریخچه

نخستین نتیجه بدست آمده در مورد رنگ آمیزی گراف از تلاش های صورت گرفته روی گراف مسطح برای حل مسئله رنگ آمیزی نقشه بدست می آید .

در آن زمان فرانسیس گوتری ادا می کرد که رنگ آمیزی نقشه کلیه ایالت های بریتانیا را روی نقشه به صورتی که هیچ کدام از دو ایالت مجاور باهم هم رنگ نشوندمی تواند با 4 رنگ انجام دهد (شرط کافی).

برادر گوتری این مسئله را برای معلم ریاضی خود شخصی به نام آگوستوس دو مورگان در کالج دانشگاهی ارسال کرد .

این مرد مسئله فوق را در سال 1852 میلادی در نامه ایی که به ویلیام همیلتون نوشته بود مطرح کرد و در سال 1879 آرتور کیلی این مسئله را در انجمن ریاضی شهر لندن مطرح کرد .

آلفرد کمپ در همان سال نتایج بدست آمده را منتشر کرد و برای یک دهه تصور کرد که این مسئله حل شده است و برای تلاش های کمپ در این حوزه او به عنوان یکی از اعضای جامعه سلطنتی و پس از آن به عنوان ریاست انجمن ریاضی لندن انتخاب شد.

در سال 1890 Heawood ادعا می کرد که استدلال کمپ اشتباه است و اثبات این مسئله را برای 5 رنگ منتشر کرد . در قرن معاصر او تلاش ها فراوانی برای اثبات روش های رنگ آمیزی نقشه با تعداد 4 رنگ انجام داد که در نهایت سال 1976 توسط Wolfgang Haken و Kenneth Apple این مسئله به کمک ایده های خودکمپ و Heawood انجام شد که در آن زمان به علت استفاده از کامپیوتر برای اثبات مسئله به شدت رد شد.

رنگ آمیزی گراف از اوایل دهه 70 به عنوان یک مسئله الگوریتمی بررسی شد و طوری که جز یکی از 21 مسئله NP-Compelet که karp معرفی کرد.

الگوریتم

می توان برای این مسئله از روش انشعاب و حد استفاده کنید. می دانیک که گراف را می توان با Δ+1 رنگ آمیزی کرد پس B=Δ+1 می تواند کران اولیه را برای شروع جستجو باشد .

از آنجایی که هیچ 2 راس مجاوری رنگ یکسان ندارند به عبارتی دیگر قصد داریم گراف را به χ(G) مجموعه مستقل افراز کنیم .

در هر مرحله معمولا یکی زیر مجموعه مستقل ماکسیمال را که هنوز رنگ نشده را به رنگ جدید در می آوریم و باقی گراف را به صورت بازگشتی رنگ می کنیم و در صورت خارج شدن از کران به دست آمده به مرحله قبل برمی گردیم.

از آنجایی که به ازای هر ترتیب رنگی این مجموعه روش به جواب های مشابهی می رسد ، فرضا این مجموعه ها را از بزرگ به کوچک رنگ می کنیم می دانیم اگر بخواهمی در کتر از B مرحله گراف را رنگ آمیزی کنیم باید براساس لانه کبوتری در یک مرحله n/B راس را رنگ کنیم .

از آنجایی که ترتیب رنگ ها را از بزرگ به کوچک در نظر بگیریم در هر مرحله باید مجموعه به صورت مستقل انتخاب شود و حداقل |V′|/B عضو داشته باشد ،مجموعه راس های رنگ نشده V′ است .

• الگوریتم براساس موارد زیر انجام می شود :
• تا زمانی که هنو راس رنگ نشده وجود ندارد.
• به ازای هر مجموعه مستقل ماکسیمال گراف مثلا α
• زمانی که سایز α از مجموعه مستقل سابق بزرگ تر باشد برای جلوگیری از شمردن حالت تکرار آن را ترک می کنیم .
• در صورتی |α|>n/(B−k) آن را رنگ k+1 در می آوریم و K یک واحد زیاد می کنیم .
• در غیر این صورت α نمی تواند به افراز اضافه می شود و به سراغ مجموعه مستقل بعدی خواهیم رفت .
• در نهایت عدد K نشان دهنده تعداد رنگ های استفاده شده خواهد بود .

پییچیدگی الگوریتم

پیچیدگی این الگوریتم O(Δn) است اما در صورتی که مسئله با برنامه نویسی پویا صورت می گیرد یعنی مقدار χ(G′) برای هر زیر گراف القایی بعد از یک بار محاسبه ذخیره شود پیچیدگی از O(4n) خواهد بود.

کاربردهای مساله رنگ آمیزی گراف

مساله رنگ آمیزی گراف دارای کاربردهای بسیار زیادی می باشد که در زیر به برخی از آن اشاره می کنیم

برنامه ریزیی جدول زمانی : فرض می شود که قرار است برنامه امتحانات یک دانشگاه را تنظیم کنید لیستی از موضوعات متفاوت در آن وجود دارد و دانشجویان گوناگونی دروس مختلف را ثبت می کنند .

اکثر دانشجویان دروس مشترک را انتخاب می کنند (در حقیقت برخی از دروس ، دانشجویانی مشترک دارند) .

به چه شکل می توان امتحانات را به گونه ای برنامه ریزی کرد که هیچ کدام از دو امتحان برای یک دانش آموز به صورت مشترک در یک زمان واحد برایش انجام نشود؟

حداقل بازه زمانی که برای برگزاری امتحانات نیاز است چه اندازه است ؟

این مساله را می توان به عنوان مساله گراف نشان داد و در آن هر راس یک موضوع و هر یال بین دو راس را که به معنی وجود دانش آموز مشابه است .

پس برنامه ریزی جدول زمانی امتحانات یک مساله رنگ آمیزی گراف می باشد که در آن حداقل بازه زمانی با عدد کروماتیک گراف برابر است .

تخصیص فرکانس رادیویی موبایل : زمان تخصیص فرکانس های رادیویی به برج ها ، این شرط موجود است که فرکانس های تخصیص یافته به سایر برج ها در موقعیت یکسان باید متفاوت باشد.

چگونه می توان فرکانس ها را با این محدودیت تخصیص داد ؟ حداقل فرکانس موردنیاز چقدر است ؟ این مساله نیز نمونه ای از مسائل رنگ آمیزی گراف بشمار می رود که در آن هر برج نشان دهنده یک راس و یال بین دو برج نشانگر آن می باشد که آن ها در رنج هم قرار می گیرند.

سودوکو : سودوکو نوعی از مسائل رنگ آمیزی گراف محسوب می شود که د آن هر سلول نشان دهنده یک راس است و اگر راس ها در سطر و ستون یا بلوک مشابهی قرار گیرند، یک یال بین آن ها موجود است .

تخصیص ثبات : در بهینه سازی کامپایلر ، «تخصیص ثبات» (Register Allocation) فرآیند تخصیص تعداد بالایی از متغیرهای برنامه هدف در تعداد کمی از ثبات های «واحد پردازش مرکزی» می باشد . یکی از مسائب رنگ آمیزی گرف بشمار می رود.

گراف دو بخشی : می توان با رنگ آمیزی گراف و استفاده از دو رنگ آن را بررسی کرد آیا گراف دو بخشی است زمانی که بتوان گراف را تنها با دو رنگ رنگ آمیزی کرد گراف دو بخشی خواهد بود .

رنگ آمیزی نقشه : رنگ آمیزی نقشه های جغرافیایی کشورها یا شهرهای یک کشور به طوریکه هیچ دو کشور یا شهر نزدیک به هم دارای رنگ مشابه نباشند؛ یکی از مسائل رنگ آمیزی گراف محسوب می شود .

براساس «قضیه چهار رنگ»(Four Color Theorem) برای رنگ آمیزی هر نقشه به طوریکه هیج کدام ازدو کشور یا شهر نزدیک به هم مدارای رنگ های مشابه نباشد و فقط رنگ کافی است .

در نقشه های ساده تر ، فقط سه رنگ کافی است و از رنگ چهارم برای بعضی نقشه ها استفاده می شود.

سایر کاربردها: مساله رنگ آمیزی گراف به صورت متعدد و متنوع نیاز دارد به عنوان مصال شبکه ایی از هزاران سرور وجود دراد که از آن ها برای توزیع محتوا در بستر اینترنت استفاده می شود.

به روز رسانی ها قادر نیستند روی تمام سرور ها به صورت همزمان اتفاق بیفتد زیرا ممکن است فعالیت سرور طی مراحل نصب متوقف شود همچنین نباید هر بار فقط یکی از سرورها به روز رسانی شود؛ زیرا زمان زیادی در برخواهد داشت .

به همین دلیل سرورهای زیادی هستند که نباید به صورت همزمان فعالیت آن ها متوقف شود؛ زیرا فعالیت های حیاتی صورت می گیرد و در عین حال به علت زمان بر بودن این فرآیند بیان شده برای تک به تک آن ها به صورت جداگانه این کار ممکن نیست .

مساله بیان شده دارای حالت متداولی از کاربرد مساله رنگ آمیزی گراف برای انجام زمان بندی است .

برای گرافی با 75000 گره فقط 8 رنگ برای رنگ آمیزی کافی است به همین دلیل در مساله به سرورهای نیز در این شرایط می توان کار را به روزرسانی را در هشت گذر صورت می گرفت .

رنگ آمیزی گراف به روش حریصانه

در مساله رنگ آمیزی راس های گراف ، زمانیکه قبل از این نیز بیان شد ، هدف رنگ کردن راس ها به صورتی است که هیچ دو راس مجاوری دارای رنگ مشابه نباشد هیچ الگوریتم کارامدی برای رنگ آمیزی گراف با حداقل رنگ های ممکن وجود ندارد و این مساله از جمله مس«ان پی کامل » (NP Complete) بشمار می رود .

«الگوریتم های تقریبی» (Approximate Algorthms) گوناگونی برای حل این مساله وجود دارند.

روش حریضانه برای مسئله حریصانه مورد بررسی قرار گرفت این روش تضمین نمی کند که کمترین تعداد رنگ ها را استفاده کند؛ اما حد بالا در تعداد رنگ ها را تضمین می کند.

الگوریتم پایه هرگز قادر نیست بیش از d+1 رنگ که در آن d برابر با درجه بیشینه راس در گراف داده شده را استفاده کند.

منابع :

ویکیپدیا

اوپدیا