درخت پوشای مینیمم یا Minimum spanning tree که به درخت پوشای کمینه نیز معروف است ، یکی از مسائل مهم در نظریه گراف می باشد.
در ادامه به بررسی جامع درخت پوشای مینیمم یا MST می پردازیم و الگوریتم ها و روشهای حل این مسئله را بررسی خواهیم کرد.
درخت پوشای مینیمم چیست؟
درخت پوشا زیرمجموعهای از گراف G است که همه رئوس آن با کمترین مقدار یالهای ممکن پوشش یافته است.
از این رو یک درخت پوشا دور ندارد و هیچ رأس ناهمبندی در آن دیده نمیشود.
به بیان ساده ، درخت پوشای کمینه یا مینیم ، درختی است که در آن هر راس گراف ، فقط یک میسر به راس های دیگر داشته باشد {نه کمتر ، نه بیشتر} ، و مجموع وزن یالها کمترین مقدار ممکن باشد.به این ترتیب اگر ما n تا راس داشته باشیم ، قطعا n-1 یال خواهیم داشت. شکل زیر میتواند به فهم بهتر مفهوم درخت پوشای میینمم کمک می کند.
تعریف درخت پوشای مینیمم :
درخت پوشای مینیمم یک درخت همبند است که مجموع وزن یال های آن کمترین مقدار باشد.
درخت همبند ، درختی است که بین هر دو راس دلخواه آن ، حداقل یک مسیر وجود داشته باشد.
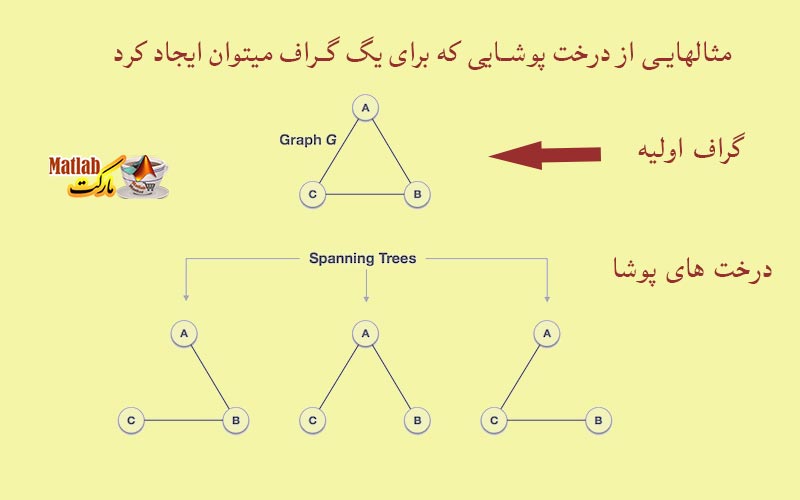
همانطور که میدانید ، برای یک گراف داده شده G ممکن است چندین درخت پوشا وجود داشته باشد ، از بین درخت های پوشای مختلفی که میتوان برای گراف G ساخت، درخت پوشایی که جمع وزن یالهای آن کمترین مقدار باشد را درخت پوشای مینیمم میگویند.
مساله کوچکترین درخت پوشا به صورت یک مساله بهینه سازی گسسته باینری (صفر و یک) بیان شده است
تعریف رسمی درخت پوشای مینیم :
در نظریه گراف ، برای گراف کامل G که وزن دار و بدون جهت می باشد ، یک درخت پوشا T ، درختی می باشد که شامل همه راس های گراف باشد و همچنین شامل کمترین تعداد یال های ممکن.
به عبارت دیگر باید گفت، درخت پوشای T درختی می باشد که، مجموعهای از یالها را شامل میشود که آن یالها تمام رئوس را پوشش میدهد.
در حقیقت همه راس های گراف G در درخت پوشا وجود دارند ، به شرطی که هیچ حلقه یا دوری ایجاد نشود ، و درخت همبند نیز باشد.
درخت پوشای کمینه (Minimum Spanning Tree) یک درخت پوشا می باشد که داری کمترین هزینه باشد. منظور از هزینه مجموع هزینه یال های درخت می باشد.
مثال زیر را در نظر بگیرید.
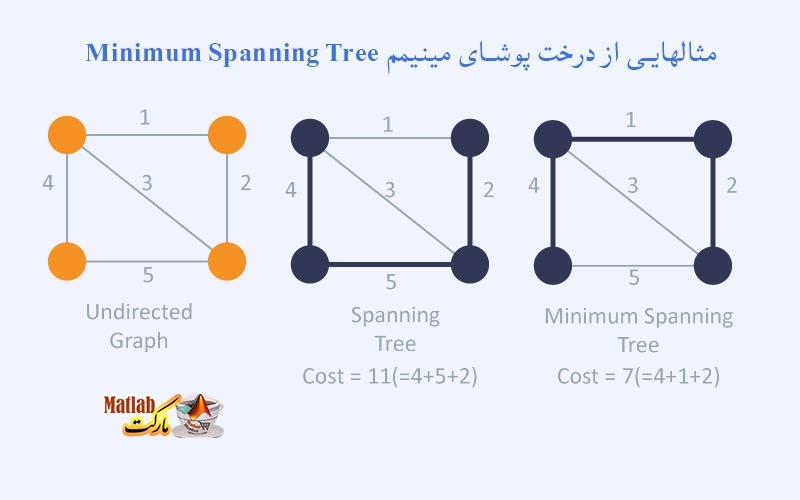
در شکل فوق گراف بدون جهت G، یک گراف وزن دار همبند می باشد.
دو گراف دیگر زیر مجموعه ای از گراف G می باشند که، شامل همه راس ها هستند و دوری در آن تشکیل نشده است.
هر دو درخت ، درخت پوشا هستند اما ، درختT اول دارای هزینه 11 و درخت دوم دارای هزینه 7 می باشد ، پس درخت پوشای دوم که هزینه کمتری دارد ، درخت پوشای مینیمم برای گراف سمت چپ می باشد.
کاربرد درخت پوشای کمینه
در مسائلی که هدف ایجاد شبکهای است که برای ایجاد ارتباط بین هر دو عضو آن هزینهای باید بپردازیم و میخواهیم در نهایت در این شبکه بین هر دو عضو ارتباط وجود داشته باشد، درخت پوشای کمینه همان کم هزینهترین شبکه است.
برای مثال فرض کنید در کشوری میخواهیم طوری جادهسازی کنیم که بتوان از هر شهری به هر شهر دیگری سفر کرد و هزینه ساخت جاده بین هر دو شهر را داریم (این هزینه میتواند تابعی بر اساس فاصله ۲ شهر، آب و هوای بین دو شهر فاصله آنها از شرکت راهسازی و … باشد). برای پیدا کردن کم هزینهترین راه، باید درخت پوشای کمینه را بیابیم.
ویژگی های درخت پوشای کمینه :
هر گراف کاملاً همبند و غیر جهتدار G دستکم یک درخت پوشا دارد.
یک گراف ناهمبند؛ هیچ درخت پوشایی ندارد، چون امکان پوشش همه رئوس آن میسر نیست.
تعداد حالات ممکن
امکان وجود بیش از یک درخت پوشای کمینه وجود دارد،
- برای مثال اگر تمام یالها وزن برابری داشته باشند، تمام زیر در ختها درخت پوشای کمینه هستند.
- اگر وزن هر دو یال با هم متفاوت باشد، تنها یک درخت پوشای کمینه خواهیم داشت.
کم وزنترین یال در برش گراف
ادعا: اگر گراف را به دو مجموعه V و V′ از راسها افراز کنیم، کموزنترین یال بین یالهایی که یک طرفشان در مجموعه V و طرف دیگرشان در مجموعه V′ است باید جزء درخت پوشای کمینه باشد. (اگر چند یال با کمترین وزن وجود داشت، باید دقیقاً یکی از آنها جزء درخت پوشای کمینه باشد).
کموزنترین یال گراف
اگر کموزنترین یال گراف یکتا باشد در هر درخت پوشای کمینهای وجود خواهد داشت.