مسئله فروشنده دوره گرد یا travel salesman problem ، یکی از مسائل کلاسیک و مهم در دنیای بهینه سازی می باشد.
[static_block_content id=”568″]
تعریف فروشنده دوره گرد :
در مسئله TSP تعدادی شهر داریم، و هزینه جابجایی بین شهر ها را نیز میدانیم ، حال میخواهیم کم هزینه ترین مسیری را که میتوانم از شهر x شروع کرده و از تمام شهر های دیگر را فقط و فقط یکبار عبور کنیم و مجدد به شهر x برگردیم را پیدا کنیم.
برای فهم بهتر مسئله شکل زیر مشاهده کنید : در این تصویر تعدادی شهر را در صفحه نمایش داده ایم ، اما هدف این است که مسیری برای گذشتن از همه این شهر ها پیدا کنیم طوری که از هر شهر فقط یک بار بگذریم.
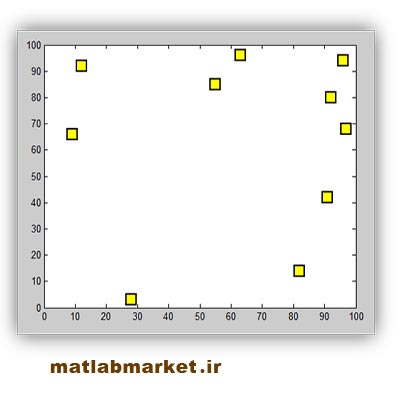
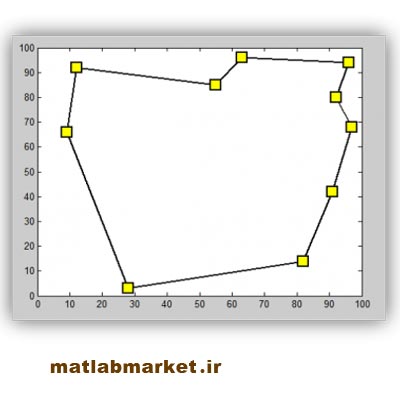
برای مثال شکل زیر را در نظر بگیرید. میخواهیم کوتاهترین مسیر را با شروع از یک شهر دلخواه و بازگشت به آن پیدا کنیم.
برای حل مسئله فروشنده دوره گرد ، از الگوریتم های فراابتکاری استفاده میشود . اما از انجا که برخی از الگوریتم های فراابتکاری گسسته و برخی دیگر پیوسته هستد ، نیاز به کد کردن مسئله TSP متناسب با الگوریتم مورد نظر می باشد.
سه روش کلی برای کد کردن راه حلهای مسئله TSP ارائه شده است که در الگوریتمهای مختلفی قابل استفاده هستند. راه حلهای سهگانه عبارتند از:
- نمایش راه حل بصورت یک رشته گسسته جایگشتی
- نمایش راه حل بصورت یک کلید تصادفی یا Random Key
- نمایش راه حل بصورت ماتریس های شبه فرمون
در ادامه هر یک از این روشهای کدینگ مسئله TSP را تشریح خواهیم کرد.
نمایش جواب فروشنده دوره گرد بصورت رشته گسسته جایگشتی : در الگوریتم هایی که عملگرهای انها به ما اجازه استفاد ه از جایگشت را میدهند بهتر است که کدینگ راه حل tsp را بصورت جایگشتی در نظر بگیریم.
از جمله این الگوریتم ها میتوان به موارد زیر اشاره کرد (اینها الگوریتم های بهینه سازی گسسته هستند):
- الگوریتم ژنتیک یا Genetic Algorithms (به اختصار GA)
- شبیهسازی تبرید یا Simulated Annealing (به اختصار SA)
- جستجوی ممنوعه یا Tabu Search (به اختصار TS)
- جستجوی همسایگی متغیر یا Variable Neighborhood Search (به اختصار VNS)
- بهینهسازی کلونی مورچگان یا Ant Colony Optimization (به اختصار ACO)
- جستجوی هارمونی یا Harmony Search (به اختصار HS)
نکته مهم در این نوع کد کردن راه حل بصورت جایگشتی ، این است که در حین مراحل الگوریتم خاصیت جایگشت درراه حل ها حفظ شود.
ب) نمایش جواب به صورت کلیدهای تصادفی یا Random Key : در الگوریتم های بهینه سازی پیوسته ، از آنجا که امکان استفاده از رشته جایگشتی وجود ندارد و پاسخ ها بصورت اعداد حقیقی می باشند نه گسسته ، پس باید از روش دیگری استفاده کرد که روش کلید تصادفی گزینه مناسبی است.
استفاده از روش کلید تصادفی در الگوریتم های بهینه سازی پیوسته در در زیر به برخی از آنها اشاره میکنیم مرسوم است:
- الگوریتم ژنتیک پیوسته یا Genetic Algorithms (به اختصار GA)
- بهینهسازی ازدحام ذرات یا Particle Swarm Optimization (به اختصار PSO)
- الگوریتم رقابت استعماری یا Imperialist Competitive Algorithm (به اختصار ICA)
- تکامل تفاضلی یا Differential Evolution (به اختصار DE)
- بهینهسازی مبتنی بر جغرافیای زیستی یا Bio-geography Based Optimization (به اختصار BBO)
- استراتژیهای تکاملی یا Evolution Strategies (به اختصار ES)
- برنامهریزی تکاملی یا Evolutionary Programming (به اختصار EP)
نمایش راه حل tsp به شکل ماتریسهای شبیه فرومون که توسط تمامی الگوریتمهای بهینه سازی پیوشته که در بالا اشاره کردیم قابل استفاده است .
مسئله فروشنده دوره گرد و نظریه گراف
مسئله معادل در نظریه گراف به این صورت است که یک گراف وزندار کامل داریم که میخواهیم کموزنترین دور همیلتونی را پیدا کنیم.
مسئله تنگراه فروشنده دورهگرد (به انگلیسی: Bottleneck traveling salesman problem، بهاختصار: bottleneck TSP) مسئلهای بسیار کاربردی است که در یک گراف وزندار کموزنترین دور همیلتونی را میخواهد که شامل سنگینترین یال باشد.
تعمیمیافته مسئله فروشنده دورهگرد دارای ایالتهایی است که هر کدام حداقل یک شهر دارند و فروشنده باید از هر ایالت دقیقاً از یک شهر عبور کند. این مسئله به «مسئله سیاستمدار مسافر» نیز شهرت دارد.
فروشنده دوره گرد احتمالی (probabilistic travelling sales man):
مساله فروشنده دوره گرد احتمالی اولین بار توسط Jaillet ارائه شده است. که در هر نمونه از مسئله تنها مجموعهای از شهرها حضور دارند.
همان مسئله فروشنده دوره گرد معمولی بوده است در حالی که تعداد گره ها (شهرها) یی که در هر تور ملاقات میکند، زیر مجموعهای از تور اولیه میباشد. در واقع به این معنی است که تعداد شهرها در هر زمان یک متغیر تصادفی محسوب میشود.
و هدف این مساله این است که اولا تور اولیه با کمترین طول را پیدا کرده و ثانیا اگر هر زیر مجموعه تصادفی از شهرها، با همان ترتیبی که در تور اولیه ظاهر شدهاند، بازدید شود، کمترین طول را داشته باشد.
مهمترین تفاوت PTSP با TSP در این است که در مسئله فروشنده دوره گرد احتمالی، احتمال ملاقات هر گره بین صفر و یک میباشد در حالی که در مسئله فروشنده دوره گرد معمولی احتمال ملاقات هر گره، یک میباشد. در یک نمونه داده شده از مسئله، گرههای موجود باید بر اساس ترتیب تور اولیه ملاقات بشوند، در حالی که از سایر گرهها میتوان به راحتی صرفه نظر نمود.
منبع : ویکی پدیا
