مسئله پیدا کردن کوتاه ترین مسیر در گراف یا شبکه

در مسئله پیدا کردن کوتاه ترین مسیر در گراف ،  ما یک گراف داریم (که میتواند یک شبکه یا هر چیز مشابه ای باشد) و هدف ما پیدا کردن کوتاه ترین مسیر بین گره مبدا و گره مقصد می باشد.

یعنی میخواهیم کوتاهترین مسیر بین دو گره مورد نظر در گراف را پیدا کنیم.

مسئله پیدا کردن کوتاه ترین مسیر در گراف

در نظریه گراف ها مسئله یافتن کوتاه ترین مسیر در حقیقت مسئله یافتن مسیری بین دو راس یا گره می باشد به گونه ای که مجموعه وزن یال ها تشکیل دهنده آن کمینه شود به عنوان مثال می توان مسئله یافتن سریع ترین راه برای رفتن از مکانی به مکانی دیگر روی نقشه را در نظر گرفت در این حالت راس ها نشان دهنده مکان و یال ها نشان دهنده قسمت های مسیر است که براساس زمان لازم برای طی کردن آن وزن گذاری خواهد شد .

اگر یک گراف وزن دار که شامل مجموعه V از رئوس ، مجموعه E از یال ها و تابع وزن f : E → R است . یک عنصر مانند V از مجموعه V داشته است .

هدف پیدا کردن مسیری مانند P از V به ‘v است به گونه ای که کوتاه ترین مسیر بین کلیه مسیرهای موجود از V به ‘v hsj .

این مسئله گاهی تحت عنوان مسئله یافتن کوتاه ترین مسیر بین دو راس نام گذاری شده است و تا سایر حالت های کلی به صورت زیر است :

مسئله یافتن کوتاه ترین مسیر از مبدا واحد که در آن هدف پیدا کردن کوتاه ترین مسیر از راس مبدا V تا تمامی رئوس دیگر در گراف است .

مسئله یافتن کوتاه ترین مسیر به مقصد واحد که در آن هدف پیدا کردن کوتاه ترین مسیر از کلیه رئوس گراف تا راس مقصد V است .

مسئله یافتن کوتاه ترین مسیر بین هر دو راس که در آن هدف یافتن کوتاه ترین مسیر بین هر جفت راس V و ‘v در گراف است.

این حالت به صورت معنا داری نسبت به مسئله موردنظر از الگوریتم های کارآمدتری برخوردار می باشند.

الگوریتم ها

مهم ترین الگوریتم ها برای حل مسئله عبارتند از :

الگوریتم دیکسترا : مسئله یافتن مسیر بین دو راس ، از مبدا واحد به مقصد واحد را حل می کند.

الگوریتم بلمن – فورد: مسئله یافتن کوتاه ترین مسیر از مبدا واحد را در حالتی حل می کند که وزن یال ها منفی هم می تواند باشد

الگوریتم جستجوی آ : با کنک روش های ابتکاری جستجو، این مسئله بین دو راس را تسریع می بخشد.

الگوریتم فلوید- وارشال : این مسئله را بین دو راس حل می کند.

الگوریتم جانسون : مسئله یافتن کوتاه ترین مسیر بین دو راس را حل کرده و در گراف های پراکنده ممکن است سریع تر ازفلوید – وارشال عمل کند.

نظریه بی نظمی ها : کوتاه ترین مسیر محلی را پیدا می کند.

کاربردها

مسئله یافتن کوتاه ترین مسیر برای یافتن مسیرهای میان مکان های واقعی از قبیل راه های عبور و مرور در نقشه های اینترنت مثل گوگل استفاده می شود.

اگر بخواهیم یک ماشین مجازی غیرواقعی را به صورت گراف در نظر بگیریم که در آن راس ها نشان دهنده حالت ها و یال ها بیان کننده گذار از حالتی به حالتی دیگر باشند؛ می توان از الگوریتم یافتن کوتاه ترین مسیر به عنوان ابزاری برای پیدا کردن دنباله بهینه از انتخاب ها به منظور رسیدن به حالن ویژه بهره مند شد .

همچنین از این الگوریتم می تون برای پیدا کردن دنباله بهنیه از انتخاب ها به منظور رسیدن به یک حالت ویژه استفاده کرد.

همچنین می توان این الگوریتم را به منظور دست یابی به یک کران پایین از زمان موردنیاز برای رسیدن به یک حالت مشخص استفاده کرد .

به عنوان مثت اگر راس ها نشان دهنده یک پازل مانند مکعب رابیک و هر یال جهت دار نشان دهنده یک حرکت یا چرخش باشد می توان از الگوریتم های کوتاه مدت مسیر استفاده کرد به شکلی که این الگوریتم ها به راه حلی با کمترین تعداد حرکت منجر شوند.

زمانی در ساختار شبکه های ارتباطی یا شبکه های مخابراتی از این مسئله با عنوان مسئله یافتن کم تاخیر ترین مسیر یا د کرد اغلب ارتباط تنگاتنگی با مسئله یافتن عریض ترین مسیر دارد .

کوتاه ترین مسیر در گراف

در این مسئله هدف یافتن کوتاه ترین مسیر بین رئوس گراف ها است .

کوتاه ترین مسیر یک مبدا

اگر راس مبدا مشخص شود و کوتاه ترین راس از این مبدا تا کلیه راس ها موردنظر باشد ، این مسئله با یک مبدا است .

الگوریتم دایکسترا

این الگوریتم از نوع حریصانه است و برای گراف هایی که دارای وزن یال های منفی است کار می کند در ابتدا به راس مبدا فاصله 0 میدهیم . بعبارتی آرای dist مقدار راس شروع را 0 می گذاریم .

بعد به ازای یال های خارجی از این راس ، اگر مجموع فاصله این راس تا مبدا (dist) و یال طی شده از فاصله قبلی آن راس کمتر شود مقدار جدید را جای آن قرار خواهیم داد تا یال های خروجی همع راس ها را بررسی کند.

دلیل صحت این الگوریتم این است که کوتاه ترین فاصله یک راس تا مبدا ، کوتاه ترین فاصله راس قبل از آن به علاوه یال بین آن ها است؛ که این همان انتخاب حریصانه است .

یکی از چالش های مربوط بi الگوریتم کلونی مورچه ها در حل مسئله کوتاه ترین مسیر در گراف

مسئله کوتاه ترین مسیر در گراف : گمان کنید ما یک گراف داریم که شامل چندین گره است و مسیرهای آن بین این گره ها موجود است که به آن ها یال گفته می شود.

هر یال در حقیقت فاصله بین دوتا گره است در این گراف دو گره خاص موجود است ، گره مبدا (source) و گره مقصد(destination) . هدف مسئله ما این است که مسیر را از گروه مبدا به گروه مقصد بیابیم که دارای کمترین مسافت است .

مسافت برابر است با مجموع طول یال ها که از گره مبدا تا گره مقصد طی می شود .

دقت کنید ممکن است بین برخی از گره ها در گراف مسیر یالی موجود نباشد .

اکنون فرض کنید ما گراف زیر را داریم .

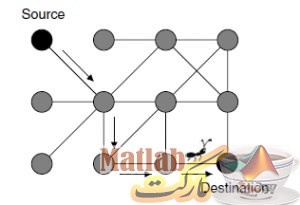
در گراف فوق مبدا، گره مقصد و کوتاه ترین مسیر از مبدا به مقصد مشخص است .

زمانی که ما بخواهیم مسئله کوتاه ترین مسیر را در این گراف با الگوریتم کلونی مورچگان حل کنیم گره مبدا معادل لانه مورچه است و گره مقصد معادل غذا است .

مورچه ها باید تلاش کنند از بین مسیرهای فراوانی که بین لانه تا غذا است کوتاه ترین مسیر را بیابند.

مهم ترین تفاوت این مسئله با مثال هایی که در قبل بیان شد این است که در آن مسائل دو مسیر به صورت مجرا از هم داشتیم و این مسیرها غیر از دو نقطه یعنی منبع و مقصد هیج نقطه مشترکی با هم ندارند بعبارتی دیگر کلیه مسیرها کاملا از هم مجزا هستند.

این تفاوت ها سبب می شود تا برای موچه هایی که قصد دارند این مسئله را حل کنند چالش هایی ایجاد شود.

مهم ترین این چالش ها ایجاد حلقه است بعبارتی ممکن است مورچه ها درون حلقه قرار گرفته و به دور خود می چرخند.

مسئله کوتاه ترین مسیر در شبکه

یکی از کاربردهای عملی و تئوری شبکه در حل مسائلی که در دنیا وجود دارد مربوط به حل مسئله کوتاه ترین مسیر در شبکه است در این مبحث شبکه ها مورد بررسی قرار می گیرند و گره های آن به مثابه نقاط مختلف موجود در این منطقه و شاخه ها نقش مسیرهای ارتباطی بین این نقاط را ایفا می کنند هر نقطه (گره) از این شبکه به صورت مبدا حرکت و هر نقطه (گره) را به صورت مقصد می تواند در نظر بگیرد.

هدف اصلی تعیین مسیر بین مبدا و مقصد حرکت است که اگر این مسیر برای حرکت انتخاب شود کمترین فاصله طی خواهد شد و به آن مسئله کوتاه ترین مسیر در شبکه می گویند.

شبکه های مربوط به این مطلب به دو نوع تقسیم می شوند که عبارت اند از :

• شبکه های بدون حلقه
• شبکه های دارای حلقه

هر کدام از این دو نوع شبکه در مسئله کوتاه ترین مسیر در ادامه مورد بررسی قرار می گیرد.

شبکه های بدون حلقه

این شبکه ها اغب به شبکه های برداری ساده شباهت دارند اما در این جا هر دو گره قادرند به عنوان گره های مبدا و مقصد حرکت در نظر گرفته شوند.

برای حل مسئله کوتاه ترین مسیر در این شبکه معمولا روش ساده حسی بکار گرفته می شود.

روش ساده کوتاه ترین مسیر

در این روش یک حرکت محاسباتی از گره مبدا یعنی شروع تا گره مقصد یعنی پایان صورت می گیرد.

در طی فرآیند این حرکت محاسباتی ، به هر کدام از گره ها یک کد (M) اختصاص می یابد که نشان از کوتاه ترین فاصله آن گره از گره شروع است .

فرض کنید که شماره گره آغاز برابر است با 1 و شماره گره پایان معادل n در نظر گرفته می شود و گره میانی به ترتیب صعودی شماره گذاری می شود .

شبکه های دارای حلقه

این شبکه ها دارای حلقه می باشند و به معنی این اسن که بین تعدادی از گره ها یک کمان برای رفت و یک کمان دیگر برای برگشت وجود دارد .

در این جا برای حل مسائل در شبکه های حلقه دارد مسئله کوتاه ترین مسیر دو روش را بیان می کند که عبارت است از »

روش کوتاه ترین مسیر دایکسترا

روش دیکسترا Dijkestea : این روش به نام ابداع کننده آن شناخته می شود و در آن به هر یک از گره ها دو کد اختصاص می یابد :

mi: کوتاه ترین فاصله گره i از گره مبدا حرکت تا مرحله جاری الگوریتم که به آن کد موقت داده می شود گفته می شود . ممکن است در مراحل بعدی، فاصله کوتاه ترین هم بدست آید.

Mi : کوتاه ترین فاصله مطلق گره i از گره مبدا حرکت که کد دائم نامیده می شود و در مراحل بغدی نیز فاصله کوتاه تر بدست نخواهد آمد.