الگوریتم رقابت استعماری یکی از الگوریتم های تکاملی الهام گرفته شده از انسان و اجتماعات انسانی می باشد این الگوریتم در سال ۲۰۰۷ توسط اسماعیل آتش پز معرفی شد و با ایده اصلی این الگوریتم از سیاست و مفاهیم امپراطوری و مستعمره می باشد.
جهت دریافت کد متلب الگوریتم رقابت استعماری به همراه فایل توضیحات خط به خط کد به “دانلود کد متلب الگوریتم ICA بهمراه توضیحات کد” مراجعه کنید.
الگوریتم رقابت استعماری یا Imperialist Competitive Algorithm که به اختصار ICA نامیده می شود روشی در حوزه محاسبات تکاملی است که به یافتن پاسخ بهینه مسائل مختلف بهینه سازی میپردازد.
این الگوریتم با مدلسازی ریاضی فرایند تکامل اجتماعی – سیاسی، الگوریتمی برای حل مسائل ریاضی بهینه سازی ارائه میدهد[۱]. از لحاظ کاربرد، این الگوریتم در دسته الگوریتم های بهینه سازی تکاملی همچون الگوریتم های ژنتیک (Genetic Algorithms)، روش بهینهسازی ازدحام ذرات (Particle Swarm Optimization)، الگوریتم کلونی مورچگان (Ant Colony Optimization)، الگوریتم تبرید شبیهسازی شده (Simulated Annealing) و … قرار می گیرد. همانند همه الگوریتم های قرار گرفته در این دسته، الگوریتم رقابت استعماری نیز مجموعه اولیه ای از جوابهای احتمالی را تشکیل می دهد. این جوابهای اولیه در الگوریتم ژنتیک با عنوان “کروموزوم”، در الگوریتم ازدحام ذرات با عنوان “ذره” و در الگوریتم رقابت استعماری نیز با عنوان “کشور” شناخته می شوند. الگوریتم رقابت استعماری با روند خاصی که در ادامه می آید، این جوابهای اولیه (کشور ها) را به تدریج بهبود داده و در نهایت جواب مناسب مسئله بهینه سازی (کشور مطلوب) را در اختیار می گذارد.
پایههای اصلی این الگوریتم را سیاست همسان سازی (Assimilation)، رقابت استعماری (Imperialistic Competition) و انقلاب (Revolution) تشکیل میدهند.
این الگوریتم با تقلید از روند تکامل اجتماعی، اقتصادی و سیاسی کشورها و با مدلسازی ریاضی بخشهایی از این فرایند، عملگرهایی را در قالب منظم به صورت الگوریتم ارائه میدهد که میتوانند به حل مسائل پیچیده بهینه سازی کمک کنند. در واقع این الگوریتم جوابهای مسئله بهینه سازی را در قالب کشورها نگریسته و سعی میکند در طی فرایندی تکرار شونده این جوابها را رفته رفته بهبود داده و در نهایت به جواب بهینه مسئله برساند[۲].
مقدمه
امپریالیسم، در لغت به سیاست توسعه قدرت و نفوذ یک کشور در حوزه خارج از قلمرو شناخته شده برای آن، اطلاق میشود. یک کشور میتواند کشور دیگر را به طور قانونگذاری مستقیم و یا از طریق روشهای غیر مستقیم، مثل کنترل کالاها و مواد خام، کنترل کند. مورد اخیر اغلب استعمار نو خوانده میشود[۳].
استعمار یک پدیده ذاتی در تاریخ بودهاست. استعمار در مراحل ابتدایی، به صورت نفوذ سیاسینظامی در کشورها و به صورت صرف استفاده از منابع زمینی، انسانی و سیاسی بودهاست. بعضی مواقع نیز استعمار، به صرف جلوگیری از نفوذ کشور استعمارگر رقیب انجام میشد. به هر حال کشورهای استعمارگر رقابت شدیدی را برای به استعمار کشیدن مستعمرات همدیگر نشان میدادند[۴].
مستقل از اثرات و تبعات مثبت و منفی آن، استعمار به عنوان یک فرایند ذاتی در تاریخ بشر ایجاد شد، و در عین وارد کردن خسارتهای جبران ناپذیر به زیربناهای اساسی یک کشور (خصوصاً زیربناهای فرهنگی) در بعضی موارد اثرات مثبتی را نیز برای کشورها مستعمره داشت[۵].
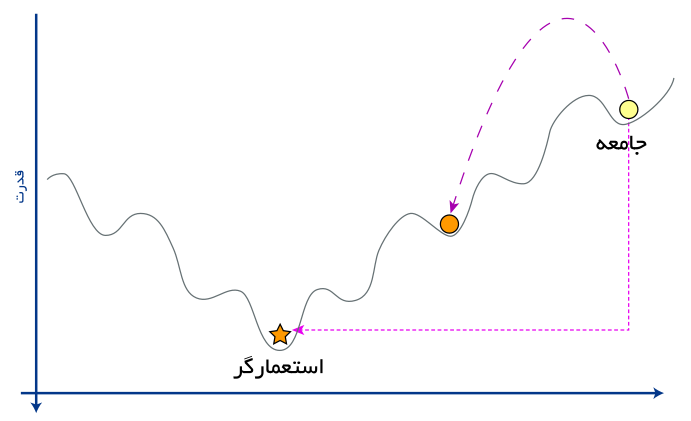
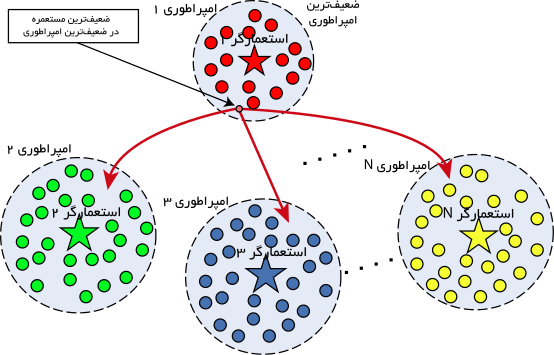
از دید بهینهسازی، استعمار بعضی از کشورها را که در یک دره معمولی تمدن قرار داشتند، خارج کرده و آنها را به یک حوزه مینیمم دیگر برد که در بعضی موارد وضعیت این حوزه مینیمم بهتر از موقعیت قبلی کشور مستعمره بود. اما به هر حال این حرکت مستلزم پیشروی مستعمره در راستای محورهای مختلف اقتصادی و فرهنگی به سمت یک امپریالیست قویتر بود، یعنی از میان رفتن بعضی از ساختارهای فرهنگی و اجتماعی. شکل زیر حرکت یک مستعمره به سمت استعمارگر قوی را نشان می دهد. این روند در الگوریتم رقابت استعماری در قالب سیاست جذب مدلسازی می شود.
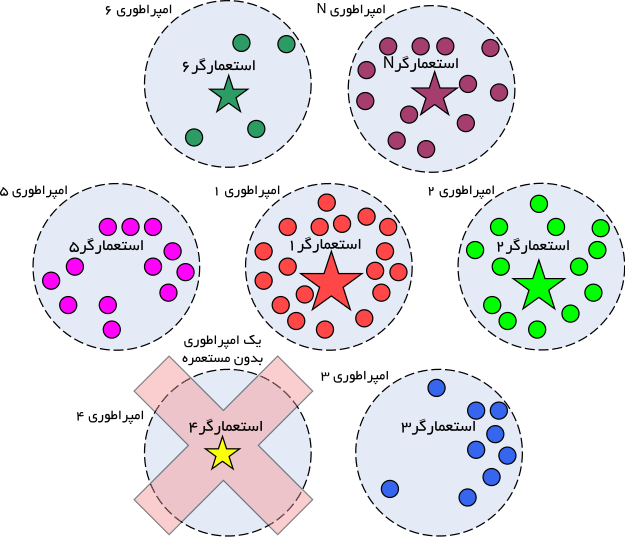
همانند دیگر الگوریتمهای تکاملی، این الگوریتم، نیز با تعدادی جمعیت اولیه تصادفی که هر کدام از آنها یک «کشور» نامیده میشوند؛ شروع میشود. تعدادی از بهترین عناصر جمعیت (معادل نخبهها در الگوریتم ژنتیک) به عنوان استعمارگر انتخاب میشوند. باقیمانده جمعیت نیز به عنوان مستعمره، در نظر گرفته میشوند.
استعمارگران بسته به قدرتشان، این مستعمرات را با یک روند خاص که در ادامه میآید؛ به سمت خود میکشند. قدرت کل هر امپراطوری، به هر دو بخش تشکیل دهنده آن یعنی کشور استعمارگر (به عنوان هسته مرکزی) و مستعمرات آن، بستگی دارد. در حالت ریاضی، این وابستگی با تعریف قدرت امپراطوری به صورت مجوع قدرت کشور استعمارگر به اضافه در صدی از میانگین قدرت مستعمرات آن، مدل شدهاست.
با شکلگیری امپراطوریهای اولیه، رقابت استعماری میان آنها شروع میشود. هر امپراطوریای که نتواند در رقابت استعماری، موفق عمل کرده و بر قدرت خود بیفزاید (و یا حداقل از کاهش نفوذش جلوگیری کند)، از صحنه رقابت استعماری، حذف خواهد شد. بنابراین بقای یک امپراطوری، وابسته به قدرت آن در جذب مستعمرات امپراطوریهای رقیب، و به سیطره در آوردن آنها خواهد بود. در نتیجه، در جریان رقابتهای استعماری، به تدریج بر قدرت امپراطوریهای بزرگتر افزوده شده و امپراطوریهای ضعیفتر، حذف خواهند شد. امپراطوریها برای افزایش قدرت خود، مجبور خواهند شد تا مستعمرات خود را نیز پیشرفت دهند.[۲]
به طور خلاصه این الگوریتم به استعمار به عنوان بخش تفکیکناپذیر از سیر تکامل تاریخی بشر نگریسته شده و از چگونگی اثرگذاری آن بر کشورهای استعمارگر و مستعمره و نیز کل تاریخ، به عنوان منبع الهام یک الگوریتم کارا و نو در زمینه محاسبات تکاملی استفاده شدهاست.
شکل دهی امپراطوریهای اولیه
در بهینهسازی، هدف یافتن یک جواب بهینه بر حسب متغیرهای مسئله، است. ما یک آرایه از متغیرهای مسئله را که باید بهینه شوند، ایجاد میکنیم. در الگوریتم ژنتیک این آرایه، کروموزوم نامیده میشود. در اینجا نیز آن را یک کشور مینامیم. در یک مسئلهٔ بهینهسازی Nvar بعدی، یک کشور، یک آرایه به طول Nvar * ۱ است. این آرایه به صورت زیر تعریف میشود.
country = [p1, p2, …, pNvar]
مقادیر متغیرهها در یک کشور، به صورت اعداد اعشاری نمایش داده میشوند. از دیدگاه تاریخیفرهنگی، اجزای تشکیل دهنده یک کشور را میتوان ویژگیهای اجتماعی– سیاسی آن کشور، همچون فرهنگ، زبان، ساختار اقتصادی و سایر ویژگیها در نظر گرفت. شکل زیر نحوه تناظر متغیر های بهینه سازی مسئله با ویژگی های اجتماعی سیاسی را نشان می دهد.

برای شروع الگوریتم، تعداد Ncountry کشور اولیه را ایجاد میکنیم. تا Nimp از بهترین اعضای این جمعیت (کشورهای دارای کمترین مقدار تابع هزینه) را به عنوان امپریالیست انتخاب میکنیم. باقیمانده Ncol تا از کشورها، مستعمراتی را تشکیل میدهند که هرکدام به یک امپراطوری تعلق دارند. برای تقسیم مستعمرات اولیه بین امپریالستها، به هر امپریالیست، تعدادی از مستعمرات را که این تعداد، متناسب با قدرت آن است، میدهیم. در شکل زیر نحوه تقسیم مستعمرات، میان کشورهای استعمارگر به صورت نمادین نشان داده شده است.[۲]
سیاست جذب: حرکت مستعمرهها به سمت امپریالیست
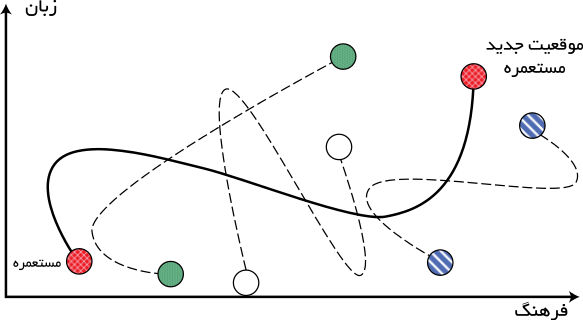
سیاست همگونسازی (جذب) با هدف تحلیل فرهنگ و ساختار اجتماعی مستعمرات در فرهنگ حکومت مرکزی انجام میگرفت. همانگونه که قبلاً نیز بیان شد، کشورهای استعمارگر، برای افزایش نفوذ خود، شروع به ایجاد عمران (ایجاد زیرساختهای حمل و نقل، تاسیس دانشگاه و …) کردند. به عنوان مثال کشورهایی نظیر انگلیس و فرانسه با تعقیب سیاست همگونسازی در مستعمرات خود در فکر ایجاد انگیس نو و فرانسه نو در مستعمرات خویش بودند. با در نظر گرفتن شیوه نمایش یک کشور در حل مسلئه بهینهسازی، در حقیقت این حکومت مرکزی با اعمال سیاست جذب سعی داشت تا کشور مستعمره را در راستای ابعاد مختلف اجتماعی سیاسی به خود نزدیک کند. این بخش از فرایند استعمار در الگوریتم بهینهسازی، به صورت حرکت مستعمرات به سمت کشور امپریالیست، مدل شدهاست.[۲]
در راستای این سیاست، کشور مستعمره (Colony)، به اندازه x واحد در جهت خط واصل مستعمره به استعمارگر (Imperialist)، حرکت کرده و به موقعیت جدید (New Position of Colony)، کشانده میشود. x عددی تصادفی با توزیع یکنواخت (و یا هر توزیع مناسب دیگر) میباشد. اگر فاصله میان استعمارگر و مستعمره با d نشان داده شود، معمولاً برای d داریم.
x ~ U(0,ß*d)
که در آن ß عددی بزرگتر از یک و نزدیک به ۲ میباشد. یک انتخاب مناسب میتواند ß=۲ باشد. وجود ضریب ß≥۱ باعث میشود تا کشور مستعمره در حین حرکت به سمت کشور استعمارگر، از جهتهای مختلف به آن نزدیک شود. همچنین در کنار این حرکت، یک انحراف زاویهای کوچک نیز با توزیع یکنواخت به مسیر حرکت افزوده میشود. یک نمای گرافیکی از اعمال سیاست جذب در الگوریتم رقابت استعماری در صفحه دو بعدی در زیر نشان داده شده است.[۲]

انقلاب؛ تغییرات ناگهانی در موقعیت یک کشور
بروز انقلاب تغییرات ناگهانی را در ویژگی های اجتماعی سیاسی یک کشور ایجاد می کند. در الگوریتم رقابت استعماری، انقلاب با جابجایی تصادفی یک کشور مستعمره به یک موقعیت تصادفی جدید مدلسازی می شود. انقلاب از دیدگاه الگوریتمی باعث می شود کلیت حرکت تکاملی از گیر کردن در دره های محلی بهینگی نجات یابد که در بعضی موارد باعث بهبود موقعیت یک کشور شده و آن را به یک محدوده بهینگی بهتری می برد.[۲]

جابجایی موقعیت مستعمره و امپریالیست
در حین حرکت مستعمرات به سمت کشور استعمارگر، ممکن بعضی از این مستعمرات به موقعیتی بهتر از امپریالیست برسند (به نقاطی در تابع هزینه برسند که هزینه کمتری را نسبت به مقدار تابع هزینه در موقعیت امپریالیست، تولید میکنند.) در این حالت، کشور استعمارگر و کشور مستعمره، جای خود را با همدیگر عوض کرده و الگوریتم با کشور استعمارگر در موقعیت جدید ادامه یافته و این این بار این کشور امپریالیست جدید است که شروع به اعمال سیاست همگونسازی بر مستعمرات خود میکند.[۲] نحوه جابجایی موقعیت مستعمره و استعمارگر در شکل زیر نشان داده شده است.
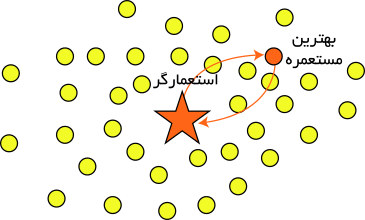
رقابت استعماری
قدرت یک امپراطوری به صورت قدرت کشور استعمارگر، به اضافه درصدی از قدرت کل مستعمرات آن تعریف میشود.
هر امپراطوریای که نتواند بر قدرت خود بیفزاید و قدرت رقابت خود را از دست بدهد، در جریان رقابتهای امپریالیستی، حذف خواهد شد. این حذف شدن، به صورت تدریجی صورت میپذیرد. بدین معنی که به مرور زمان، امپراطوریهای ضعیف، مستعمرات خود را از دست داده و امپراطوریهای قویتر، این مستعمرات را تصاحب کرده و بر قدرت خویش میافزایند.
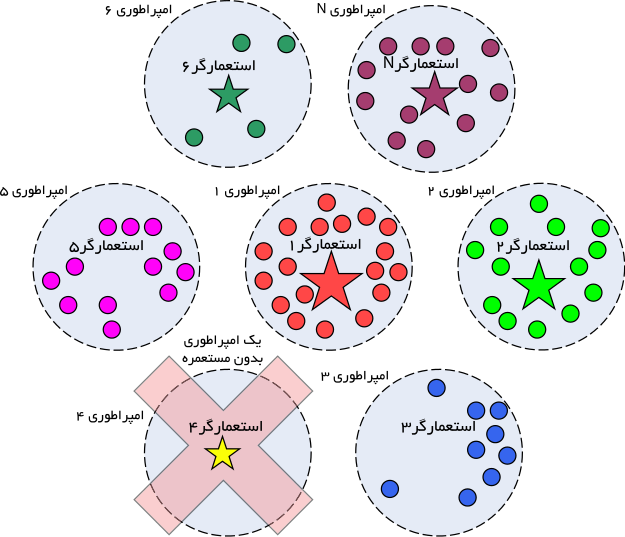
در الگوریتم رقابت استعماری، امپراطوری در حال حذف، ضعیفترین امپراطوری موجود است. بدین ترتیب، در تکرار الگوریتم، یکی یا چند مورد از ضعیفترین مستعمرات ضعیفترین امپراطوری را برداشته و برای تصاحب این مستعمرات، رقابتی را میان کلیه امپراطوریها ایجاد میکنیم. مستعمرات مذکور، لزوماً توسط قویترین امپراطوری، تصاحب نخواهند شد، بلکه امپراطوریهای قویتر، احتمال تصاحب بیشتری دارند. رقابت استعماری میان چندین استعمار گر برای جذب مستعمرات همدیگر در شکل زیر به خوبی نشان داده شده است.[۲]
سقوط امپراطوریهای ضعیف
در جریان رقابتهای امپریالیستی، خواه ناخواه، امپراطوریهای ضعیف به تدریج سقوط کرده و مستعمراتشان به دست امپراطوریهای قویتر میافتد. شروط متفاوتی را میتوان برای سقوط یک امپراطوری در نظر گرفت. در الگوریتم پیشنهاد شده، یک امپراطوری زمانی حذف شده تلقی میشود که مستعمرات خود را از دست داده باشد.[۲] شکل زیر یک نمای کلی از سقوط امپراطوری ها در روند چرخه الگوریتم، ارائه می دهد.
شبه کد
مراحل ذکر شده در بالا را میتوان به صورت شبه کد ریز خلاصه کرد.[۲]
1. چند نقطه تصادفی روی تابع انتخاب کرده و امپراطوریهای اولیه را تشکیل بده.
2. مستعمرات را به سمت کشور امپریالیست حرکت بده (سیاست همسانسازی یا جذب).
3. عملگر انقلاب (Revolution) را اعمال کن.
4. اگر مستعمرهای در یک امپراطوری، وجود داشته باشد که هزینهای کمتر از امپریالیست داشته باشد؛ جای مستعمره و امپریالیست را با هم عوض کن.
5. هزینهٔ کل یک امپراطوری را حساب کن (با در نظر گرفتن هزینهٔ امپریالیست و مستعمراتشان).
6. یک (یا چند) مستعمره از ضعیفترین امپراطوری انتخاب کرده و آن را به امپراطوریای که بیشترین احتمال تصاحب را دارد، بده.
7. امپراطوریهای ضعیف را حذف کن.
8. اگر تنها یک امپراطوری باقیمانده باشد، توقف کن وگرنه به ۲ برو.
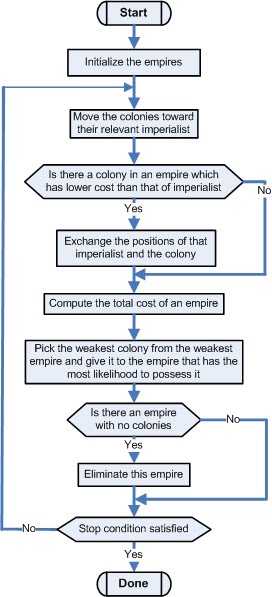
روند کامل الگوریتم رقابت استعماری را می توان با فلوچارت زیر نشان داد. نکته قابل توجه این است که در این فلوچارت، بخش انقلاب نشان داده نشده است که باید به مرحله مناسب خود اعمال گردد.
فلوچارت
کاربردها
در حالت کلی الگوریتم رقابت استعماری به هر نوع مسئله بهینه سازی بدون هیچ محدودیتی قابل اعمال است. همین موضوع باعث شدهاست تا از این الگوریتم در حل مسائل بسیاری در حوزه مهندسی برق، مکانیک، صنایع، مدیریت، عمران، هوش مصنوعی و غیره استفاده شود. به عنوان مثال از این الگوریتم با موفقیت در حل مسائل عملی بهینه سازی زیر استفاده شدهاست.
• طراحی بهینه کنترل کننده برای سیستمهای صنعتی همچون سیستم چند ورودی – چند خروجی تبرید[۶] و صنعتی ستون تقطیر[۷][۸][۹][۱۰]
• طراحی بهینه سیستمهای پیشنهاد دهی هوشمند[۱۱][۱۲]
• طراحی بهینه آنتنهای آرایهای
• حل مسائل برنامه ریزی تولید در حوزه مهندسی صنایع و مدیریت[۱۳][۱۴][۱۵]
• یادگیری و تحلیل شبکههای عصبی مصنوعی[۱۶][۱۷][۱۸]
• طراحی بهینه موتورهای القای خطی[۱۹]
• طراحی استراتژی بهینه در نظریه بازیها برای رسیدن به نقطه تعادل نش[۲۰]
• طراحی بهینه کنترل کنندههای فازی[۲۱]
• انتخاب و بهینه سازی سبد سهام[۲۲]
• طراحی و بهینه سازی ترمودینامیکی مبدل های حرارتی صفحه-پره [۲۳]
نسخههای دیگر
موارد ذکر شده در این نوشتار، مربوط به نسخه اولیه ارائه شده از الگوریتم رقابت استعماری میباشد. پس از معرفی این الگوریتم که ابتدا فقط برای حل مسائل بهینه سازی پیوسته استفاده میشد، نسخههای دیگری نیز معرفی شدند که به حل مسائل گسسته و نیز ترکیبی میپرداختند. بسیاری از مقالات و انتشارات مربوط به این الگوریتم که در آنها این نسخه معرفی شدهاند، در این لینک لیست شدهاند. به عنوان مثال نسخه آشوبی این الگوریتم توسط Duan و دیگران در یکی از مقالات بخش مراجع در زیر معرفی شده است[۲۴].
منابع
1. E. Atashpaz-Gargari, C. Lucas, Imperialist Competitive Algorithm: An algorithm for optimization inspired by imperialistic competition, IEEE Congress on Evolutionary Computation, (۲۰۰۷) ۴۶۶۱–۴۶۶۷
2. اسماعیل آتش پز گرگری، «توسعه الگوریتم بهینهسازی اجتماعی و بررسی کارایی آن»، پایان نامه کارشناسی ارشد دانشکده مهندسی برق و کامپیوتر دانشگاه تهران، ۱۳۸۷
3. R. R. Palmer, “A History of the Modern World”, New York: Alfred A. Knopf, 1964, ©۱۹۵۶٫
4. C. V. Findley & J. A. M. Rothney ,Twentieth century world, 3rd edition, Boston: Houghton Mifflin Company, 1986
5. R. Goff, J. Terry, W. Moss, J. H. Upshur, The Twentieth Century: A Brief Global History, 6th edition, Boston: McGraw-Hill , 2001, part1.
6. R. Rajabioun, F. Hashemzadeh, E. Atashpaz-Gargari, B. Mesgari, F. Rajaei Salmasi, Identification of a MIMO evaporator and its decentralized PID controller tuning using Colonial Competitive Algorithm, In the proceeding of IFAC World Congress, Seoul, Korea, 2008, pp. ۹۹۵۲-۹۹۵۷.
7. E. Atashpaz-Gargari, F. Hashemzadeh, R. Rajabioun, C. Lucas, Colonial competitive algorithm: A novel approach for PID controller design in MIMO distillation column process, International Journal of Intelligent Computing and Cybernetics. ۱(۳) (۲۰۰۸) ۳۳۷-۳۵۵.
8. E. Gargari, F. Hashemzadeh, R. Rajabioun, and C. Lucas, “Colonial competitive algorithm: A novel approach for PID controller design in MIMO distillation column process,” International Journal, vol. ۱, ۲۰۰۸
9. E. Atashpaz-Gargari and C. Lucas, “Designing an optimal PID controller using Colonial Competitive Algorithm,”
10. R. Rajabioun, E. Atashpaz-Gargari, and C. Lucas, “Colonial competitive algorithm as a tool for Nash equilibrium point achievement,” Computational Science and Its Applications–ICCSA 2008, pp. ۶۸۰–۶۹۵
11. هدی سپهری راد، «کاربرد روش های زیستی و اجتماعی در سیستم های پیشنهادگر»، پایان نامه کارشناسی ارشد دانشکده مکانیک دانشگاه تهران، ۱۳۸۶
12. H. Sepehri Rad, C. Lucas, Application of Imperialistic Competition Algorithm in recommender systems, In 13th Int’l CSI Computer Conference (CSICC’۰۸), Kish Island, Iran., ۲۰۰۸
13. زهرا رضایی، «ارائه الگوریتم فرا ابتکاری کارا برای حل مدل کنترل موجودی چند سطحی»، پایان نامه کارشناسی ارشد دانشگاه شهید بهشتی، ۱۳۸۸
14. السا شکراله پور، «زمانبندی دو معیاره سیستم مونتاژ جریان کاری دو مرحلهای توسط روشهای فرا ابتکاری»، پایان نامه کارشناسی ارشد دانشگاه شهید بهشتی، ۱۳۸۸
15. F. Jolai, M. Sangari, and M. Babaie, “Pareto simulated annealing and colonial competitive algorithm to solve an offline scheduling problem with rejection,” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture , pp. ۱–۱۳
16. امیر حسین بیابانگرد اسکویی، «تعیین خواص الاستو – پلاستیک فلزات با استفاده از آزمون سختی سطح و مطالعه اثر شکل ایندنتر در آن با استفاده از روشهای عددی و تجربی»، پایان نامه کارشناسی ارشد دانشکده مهندسی برق و کامپیوتر دانشگاه تهران، ۱۳۸۶
17. A. Biabangard-Oskouyi, E. Atashpaz-Gargari, N. Soltani, and C. Lucas, “Application of Imperialist Competitive Algorithm for Material Properties Characterization from Sharp Indentation Test,” Int J Eng Simul, vol. ۱۰, no. ۱, ۲۰۰۹.
18. T. Maryam, F. Nafiseh, L. Caro, and T. Fattaneh, “Artificial Neural Network Weights Optimization based on Imperialist Competitive Algorithm,”
19. C. Lucas, Z. Nasiri-Gheidari, and F. Tootoonchian, “Application of an imperialist competitive algorithm to the design of a linear induction motor,” Energy Conversion and Management, vol. ۵۱, no. ۷, pp. ۱۴۰۷–۱۴۱۱, ۲۰۱۰
20. R. Rajabioun, E. Atashpaz-Gargari, C. Lucas, Colonial Competitive Algorithm as a Tool for Nash Equilibrium Point Achievement, Springer Lecture Notes in Computer Science (LNCS). ۶۸۰-۶۹۵, ۲۰۰۸
21. A. Jasour, E. Gargari, and C. Lucas, “Vehicle Fuzzy Controller Design Using Imperialist Competitive Algorithm,” in Second First Iranian Joint Congress on Fuzzy and Intelligent Systems, Tehran, Iran, 2008.
22. آرش طالبی، “انتخاب و بهینه سازی سبد سهام با استفاده از روش های فراابتکاری و مقایسه ی آن با سبدهای تشکیلیِ خبرگان و تازه کارها در بازار بورس اوراق بهادار تهران”، پایان نامه دانشکده مهندسی صنایع و مدیریت دانشگاه صنعتی شاهرود، ۱۳۸۹
23. Moslem Yousefi,Amer Nordin Darus, Hossein Mohammadi, “Second law based optimization of a plate fin heat exchanger using Imperialist Competitive Algorithm, International Journal of the Physical Sciences Vol. 6(20), pp. 4749-4759, 23 September, 2011
24. . Duan, C. Xu, S. Liu, and S. Shao, “Template matching using chaotic imperialist competitive algorithm,” Pattern Recognition Letters, 2009
25. . Jain and M. Nigam, “Synergy of evolutionary algorithm and socio-political process for global optimization,” Expert Systems with Applications, 2009



نقد و بررسیها
هنوز بررسیای ثبت نشده است.